组会报告《计算机图形学渲染技术：从光栅化到路径追踪》提纲

发表于 更新于 分类于

计算机图形学渲染技术：从光栅化到路径追踪

引言

计算机图形学渲染技术是将三维虚拟场景转换为二维图像的关键过程，广泛应用于游戏、电影、科学可视化等领域。本此报告将从基本概念出发，深入探讨光栅化、光线投射、光线追踪、路径追踪等渲染技术的发展与应用。

计算机图形学渲染技术的定义与目标

  • 计算机图形学渲染技术的定义：以软件由模型生成数字图像的过程。
  • 模型的定义：用语言或者数据结构进行严格定义的三维虚拟场景的描述。
  • 数字图像包括：矢量图像和位图图像。

基本概念：相机、物体、光源

  • 相机：三维虚拟场景中相机模拟人眼或物理摄像机的视角，它决定了观察点的位置、方向和视野范围。
  • 物体：三维虚拟场景中存在的三维模型或几何体，它决定了观察的对象。
  • 光源：三维虚拟场景中发出光线的元素，它决定了物体的照明方式。

物体按照几何表示的分类（部分）

光源按照形态的分类（部分）

  • 点光源：光从一个点向所有方向发射（如灯泡）。
  • 方向光源：光线是平行的，光源被认为在无限远处（如阳光）。
  • 聚光灯：光从一个点发射，集中在一个锥形区域内（如手电光）。
  • 环境光源：全局均匀光源，照亮场景中所有物体，模拟间接光照。

基本概念：直接光照、间接光照、全局光照

光照类型 描述 示例
直接光照 光直接从光源到物体 聚光灯下物体的投影清晰
间接光照 光经反射、折射后照到物体 房间角落的柔和环境光
全局光照 场景中所有光线交互效果 真实房间中物体的自然光照
全局光照=直接光照+间接光照

不同技术的定义和特点对比

  • 技术的定义和特点对比表：
技术 定义 优缺点 性能开销 渲染效果
光栅化 将 3D 几何投影到 2D 屏幕上，将投影转化为像素图像 优点：计算成本低
缺点：不直接计算光线传播，需手动模拟反射和阴影效果		 🚀 ⭐
光线投射 从摄像机发射光线，计算与几何体的第一次交点 优点：支持直接光照
缺点：不支持反射和折射或间接光照		 🚀🚀 ⭐⭐
光线追踪 从摄像机发射光线，递归计算反射和折射 优点：支持反射和折射
缺点：间接光照效果不完善		 🚀🚀🚀 ⭐⭐⭐
路径追踪 在光线追踪的基础上随机采样光线路径，递归计算反射和折射 优点：支持全局光照（=直接光照+间接光照）
缺点：计算成本高		 🚀🚀🚀🚀 ⭐⭐⭐⭐
  • 附加选项：适用于隐式表面的渲染技术：
技术 定义 特点
光线行进 光线步进前进，使用距离估计函数，找到隐式表面或体积数据的交点 适合隐式表面或分形几何

技术详解：从光栅化到路径追踪

光栅化

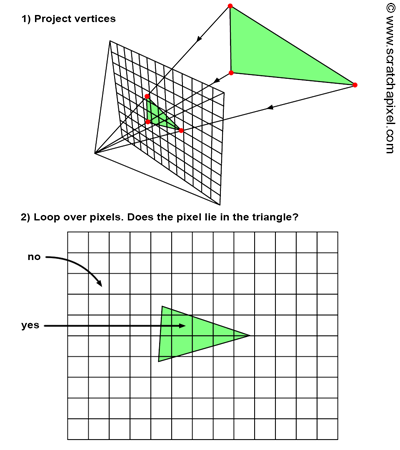
光栅化的过程分为两个主要步骤：先将空间中的物体投影到成像平面上；再遍历图像中的每一个像素，检测是否在物体的投影区域内，如果在的话就用相应颜色填充该像素。为了几何求解方便，一般选择三角面片作为光栅化中构成 3D 物体的基本图元。

upload successful upload successful

Z-Buffer：
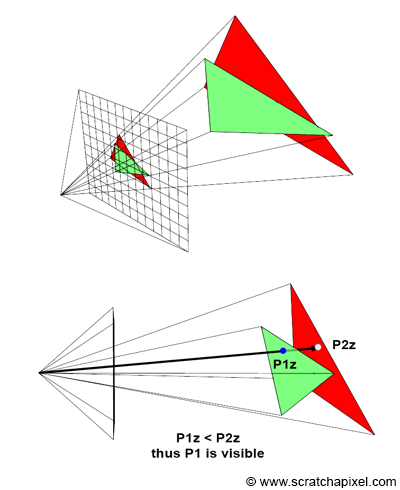
当有多个三角形相互重叠时，它们之上的某些点可能会投影到同一个像素位置，我们需要借助 z-buffer 来确定这种情况下像素用来显示哪个三角形的颜色以及其它属性。z-buffer 其实就是一个二维矩阵，用来存储每个像素对应空间物体上某一点的深度。这样就可以在重叠的情况下找出距离相机最近的一点，用于像素的着色或其它属性操作。
upload successful

光线投射

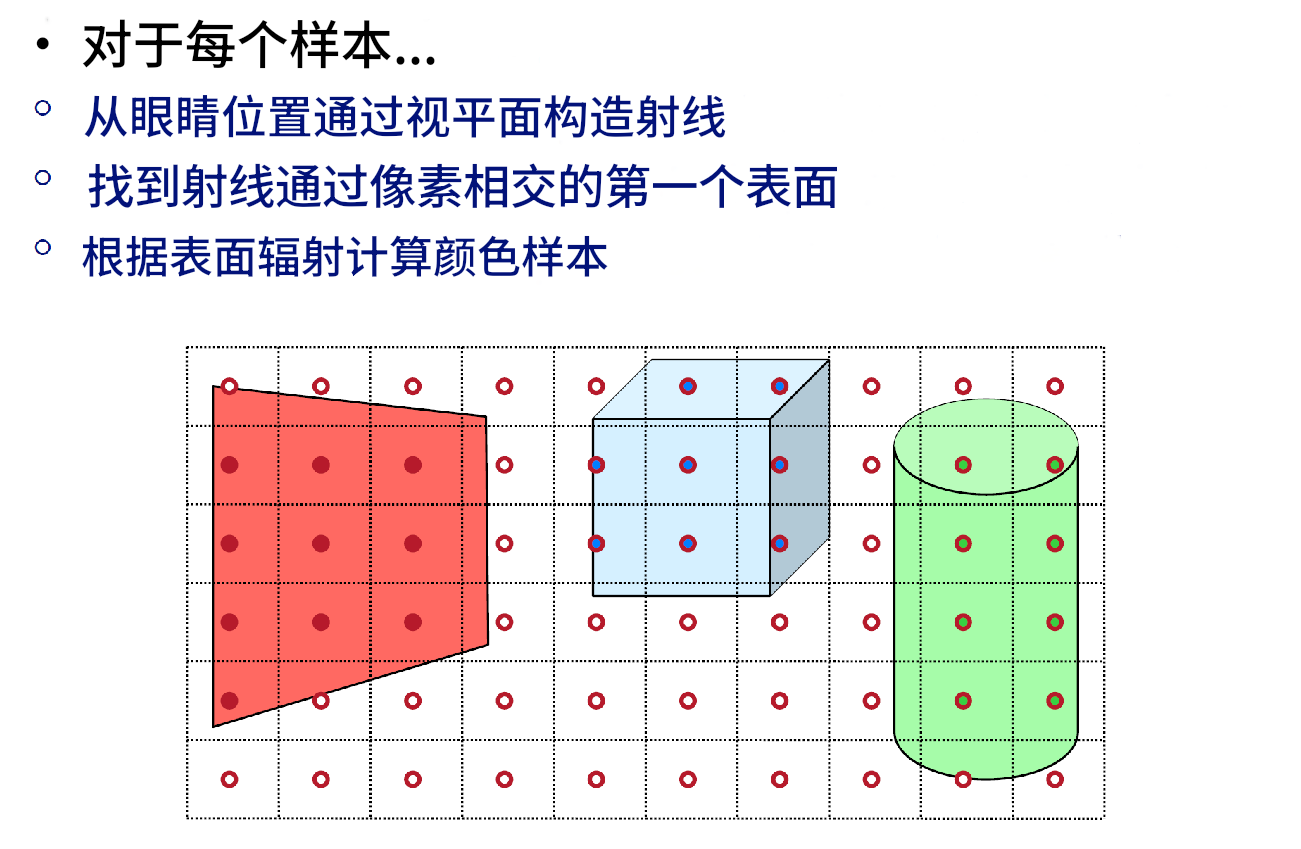
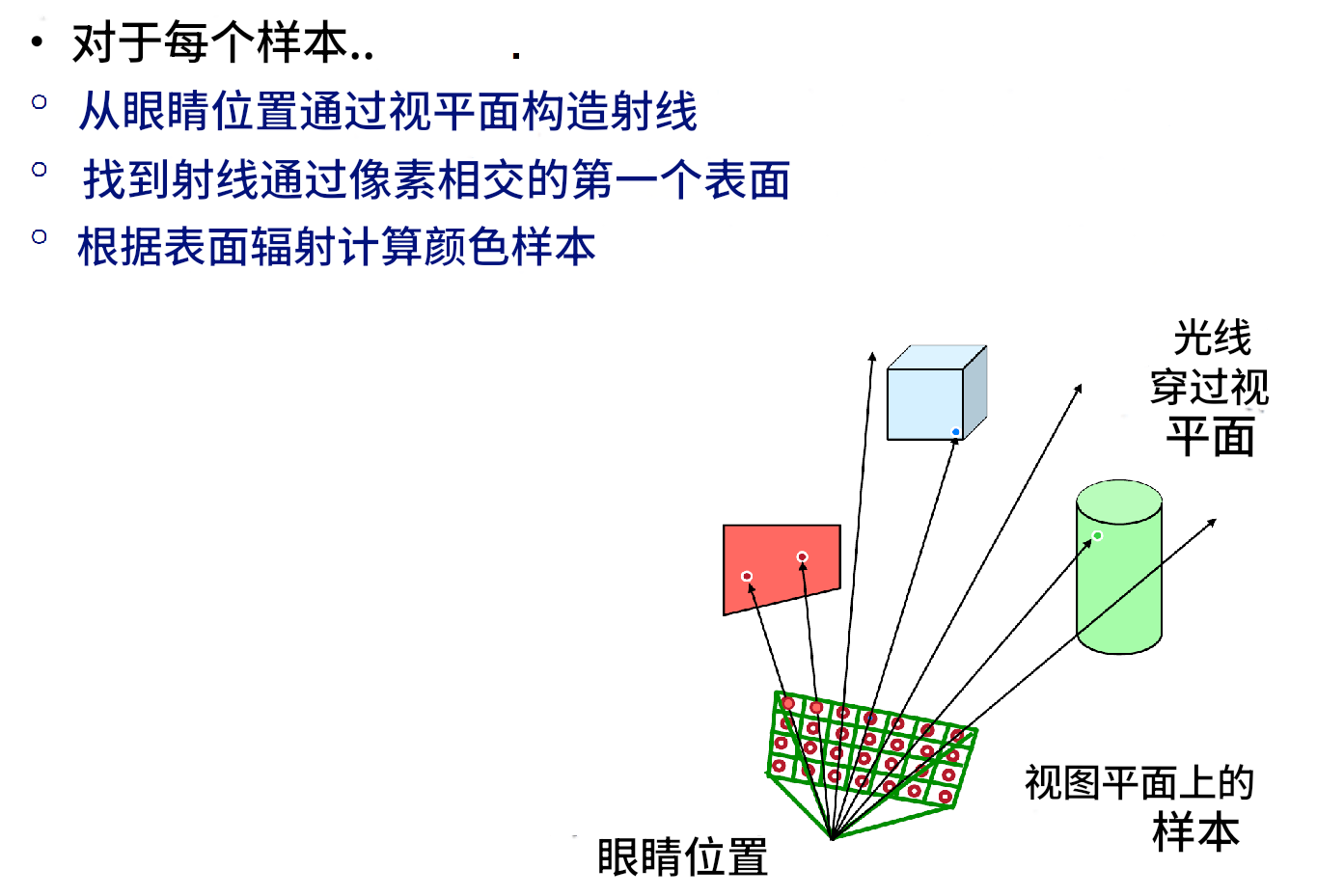
光线投射（Ray Casting）是一种基础的渲染技术，其核心思想是从相机的位置出发，通过每个像素点向场景中发射一条光线，并计算该光线与场景中物体的第一个交点。根据该交点的属性（例如材质、颜色、法线等）以及光源的分布，确定像素的最终颜色值。

光线投射的工作过程主要包括以下步骤：

  1. 光线生成：对于每个像素，定义一条从相机位置出发、穿过像素中心的光线。这些光线被用于采样三维场景中的物体。

  2. 交点计算：通过求解几何体与光线的交点方程，找到光线与场景中物体的第一次交点。若光线未与任何物体相交，则该像素渲染为空白或背景颜色。

  3. 着色计算：

    • 通过交点处的法向量计算光照信息，例如表面是否朝向光源。
    • 使用局部光照模型（如朗伯光照模型或冯氏光照模型）计算该点的颜色值，仅考虑直接光照。

upload successful
upload successful

局部光照模型概述

局部光照模型（Local Illumination Model）是计算机图形学中用来模拟物体表面光照的基本方法。它只考虑单个点与场景中直接可见的光源之间的交互，不处理光的多次反射或折射，因此计算简单且高效。局部光照模型通常包括三个光照分量：环境光照、漫反射光照和镜面反射光照。

两种经典的局部光照模型是 Phong 光照模型 和 Blinn-Phong 光照模型。它们的区别主要体现在镜面反射光的计算方法上。

光照模型的组成

1. 环境光照（Ambient Lighting）

  • 模拟从所有方向均匀分布的光照，用于模拟间接光的基本亮度。

  • 环境光的亮度与物体的环境反射特性和环境光源强度相关。

  • 公式：

    [
    I_{\text{ambient}} = k_a \cdot I_a
    ]

    其中：

    • (k_a)：材质的环境反射系数
    • (I_a)：环境光强度

2. 漫反射光照（Diffuse Lighting）

  • 模拟光线在粗糙表面上的均匀散射。

  • 漫反射光的亮度仅依赖于光源方向和表面法向量的夹角，使用朗伯余弦定律计算：

    [
    I_{\text{diffuse}} = k_d \cdot I_l \cdot \max(0, \mathbf{N} \cdot \mathbf{L})
    ]

    其中：

    • (k_d)：材质的漫反射系数
    • (I_l)：光源强度
    • (\mathbf{N})：表面法向量
    • (\mathbf{L})：指向光源的方向向量

3. 镜面反射光照（Specular Lighting）

  • 模拟光线在光滑表面上的镜面反射效应，产生高光。
  • 镜面光的亮度依赖于观察方向、光源方向和表面法向量的关系。

镜面反射的计算是 Phong 和 Blinn-Phong 光照模型的主要区别。

Phong 光照模型

在 Phong 模型中，镜面光通过光线的反射方向和观察方向之间的夹角计算：

[
I_{\text{specular}} = k_s \cdot I_l \cdot \max(0, \mathbf{R} \cdot \mathbf{V})^n
]

其中：

  • (k_s)：材质的镜面反射系数

  • (I_l)：光源强度

  • (\mathbf{R})：光线反射方向向量，定义为：

    [
    \mathbf{R} = 2 (\mathbf{N} \cdot \mathbf{L}) \mathbf{N} - \mathbf{L}
    ]

  • (\mathbf{V})：观察方向向量

  • (n)：高光的聚焦程度（值越大，高光越尖锐）。

Phong 模型的主要特点是依赖于逐像素计算反射方向向量 (\mathbf{R})，这在动态场景中可能会增加计算成本。

Blinn-Phong 光照模型

Blinn-Phong 模型对 Phong 模型进行了改进，使用半程向量（Halfway Vector） 替代反射方向向量与观察方向的夹角计算。这种方法更加高效，尤其适合动态光照场景。

镜面光的计算公式为：

[
I_{\text{specular}} = k_s \cdot I_l \cdot \max(0, \mathbf{N} \cdot \mathbf{H})^n
]

其中：

  • (\mathbf{H})：半程向量，定义为光源方向 (\mathbf{L}) 和观察方向 (\mathbf{V}) 的归一化中间方向：

    [
    \mathbf{H} = \frac{\mathbf{L} + \mathbf{V}}{||\mathbf{L} + \mathbf{V}||}
    ]

与 Phong 模型相比，Blinn-Phong 模型避免了逐像素计算反射向量 (\mathbf{R})，使镜面光的计算更加高效。此外，由于半程向量的方向更接近真实光学场景中的反射路径，Blinn-Phong 的高光区域在动态场景中更加稳定。

总光照公式

两种模型的总光照计算公式均可表示为：

[
I = I_{\text{ambient}} + I_{\text{diffuse}} + I_{\text{specular}}
]

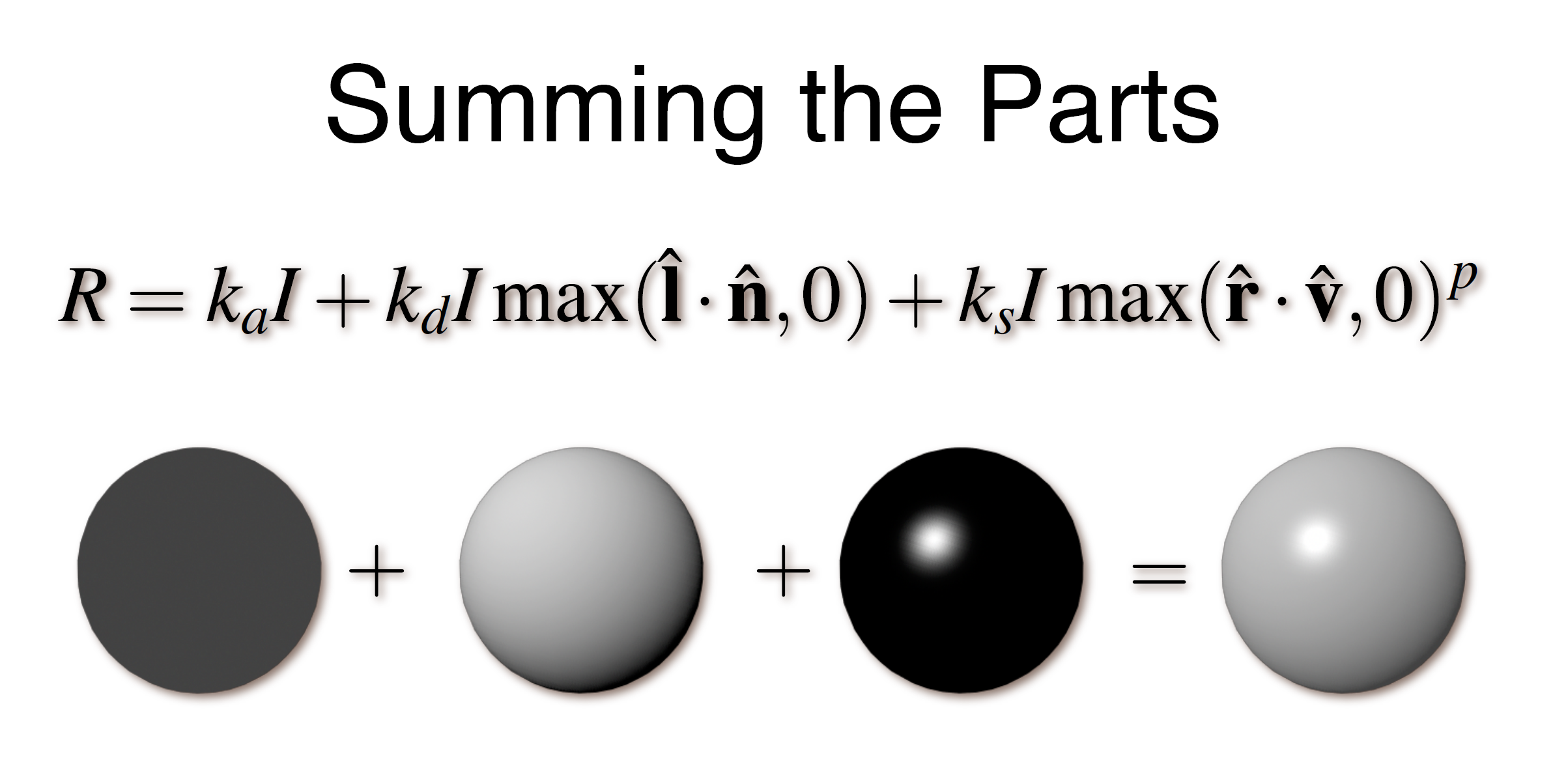
upload successful

光线追踪

在经典的光线追踪中，使用局部光照模型进行迭代的方式主要通过以下步骤实现：

  1. 光线发射和交点计算：
    从摄像机发射光线，与场景中的物体进行交点计算，找到光线与物体的第一个交点。

  2. 应用局部光照模型：
    在交点处，根据局部光照模型（如Phong或Blinn-Phong模型）计算直接光照，包括：

    • 环境光 (Ambient)
    • 漫反射光 (Diffuse)
    • 镜面反射光 (Specular)

  3. 生成次级光线：
    根据物体的材质特性，生成次级光线：

    • 反射光线：模拟光的镜面反射。
    • 折射光线（可选）：模拟透明物体的折射。

  4. 递归迭代：
    对每一条次级光线重复上述步骤：

    • 找到交点，计算局部光照。
    • 根据次级光线对最终颜色贡献的权重（如反射率或折射率），合并颜色。

  5. 停止条件：
    迭代会根据以下条件停止：

    • 光线的递归深度达到预设限制（例如5次反弹）。
    • 次级光线的能量衰减到某个阈值以下。

通过这种递归迭代，每一层的光照计算基于局部光照模型，而最终合成的图像能够模拟多次反射后的光照效果。

路径追踪

渲染方程（核心公式）

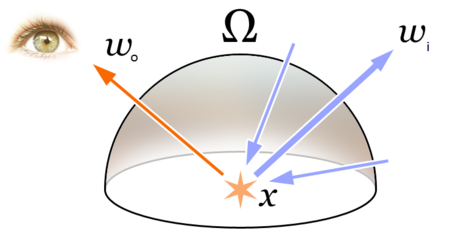
渲染方程是计算真实世界中光与物体相互作用的核心数学模型，它由 Kajiya 在 1986 年提出，是全局光照理论的基础。渲染方程描述了场景中一点的辐射亮度（radiance）如何通过其他点的辐射亮度、材质属性及几何关系计算得出。对于某个表面点 ( \mathbf{x} )，渲染方程的基本形式为：

[
L_o(\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_{\Omega} f_r(\mathbf{x}, \omega_i, \omega_o) L_i(\mathbf{x}, \omega_i) (\omega_i \cdot \mathbf{n}) \mathrm{d}\omega_i
]

其中：

  • ( L_o(\mathbf{x}, \omega_o) )：从点 ( \mathbf{x} ) 沿方向 ( \omega_o ) 发射出的辐射亮度（出射辐射亮度）。
  • ( L_e(\mathbf{x}, \omega_o) )：点 ( \mathbf{x} ) 在方向 ( \omega_o ) 的自发光亮度。
  • ( \Omega )：点 ( \mathbf{x} ) 的单位半球，代表所有可能的入射方向。
  • ( f_r(\mathbf{x}, \omega_i, \omega_o) )：双向反射分布函数（BRDF），描述入射方向 ( \omega_i ) 和出射方向 ( \omega_o ) 之间的反射概率密度。
  • ( L_i(\mathbf{x}, \omega_i) )：从方向 ( \omega_i ) 入射到点 ( \mathbf{x} ) 的辐射亮度（入射辐射亮度）。
  • ( (\omega_i \cdot \mathbf{n}) )：入射方向与法向量的夹角余弦，描述几何遮蔽的贡献。

上述方程描述了一个递归关系：入射亮度 ( L_i ) 本身又由其他点的出射亮度决定，形成了光的全局传播过程。

upload successful

路径追踪的数值方法

路径追踪是解决渲染方程的一种数值方法，通过模拟光线传播路径来估算场景中的亮度值。路径追踪的关键思想是通过随机采样对渲染方程的积分部分进行近似。

  1. 渲染方程的蒙特卡洛近似
    渲染方程的积分项可以通过蒙特卡洛方法近似为：

    [
    \int_{\Omega} f_r(\mathbf{x}, \omega_i, \omega_o) L_i(\mathbf{x}, \omega_i) (\omega_i \cdot \mathbf{n}) , \mathrm{d}\omega_i
    \approx \frac{1}{N} \sum_{k=1}^N \frac{f_r(\mathbf{x}, \omega_{i,k}, \omega_o) L_i(\mathbf{x}, \omega_{i,k}) (\omega_{i,k} \cdot \mathbf{n})}{p(\omega_{i,k})}
    ]

    其中：

    • ( N )：采样数量。
    • ( \omega_{i,k} )：通过概率密度函数 ( p(\omega_i) ) 采样得到的第 ( k ) 个方向。
    • ( p(\omega_i) )：对入射方向 ( \omega_i ) 的采样概率密度。

    蒙特卡洛积分的误差会随着 ( N ) 的增加以 ( O ( \frac{1}{\sqrt{N}} ) ) 的速率减小。

  2. 路径构造
    路径追踪通过构造光线路径 ( \mathbf{x}_0 \to \mathbf{x}_1 \to \mathbf{x}_2 \to \cdots ) 来递归计算 ( L_i )。每次路径扩展步骤包括：

    • 从当前点 ( \mathbf{x}i ) 按 ( p(\omega_i) ) 随机采样一个方向 ( \omega{i+1} )。
    • 通过光线投射找到与场景的下一个交点 ( \mathbf{x}_{i+1} )。
    • 累积路径的亮度贡献。

  3. 逐像素辐射亮度估算
    对于图像的每个像素，其亮度由视线上的辐射亮度 ( L_o(\mathbf{x}_0, \omega_o) ) 决定。路径追踪通过为每个像素模拟多条路径，将结果平均以得到最终亮度估算：

    [
    I_{\text{pixel}} \approx \frac{1}{M} \sum_{j=1}^M L_o^{(j)}(\mathbf{x}_0, \omega_o)
    ]

    其中 ( M ) 是路径样本的数量，( L_o^{(j)} ) 是第 ( j ) 条路径的亮度贡献。

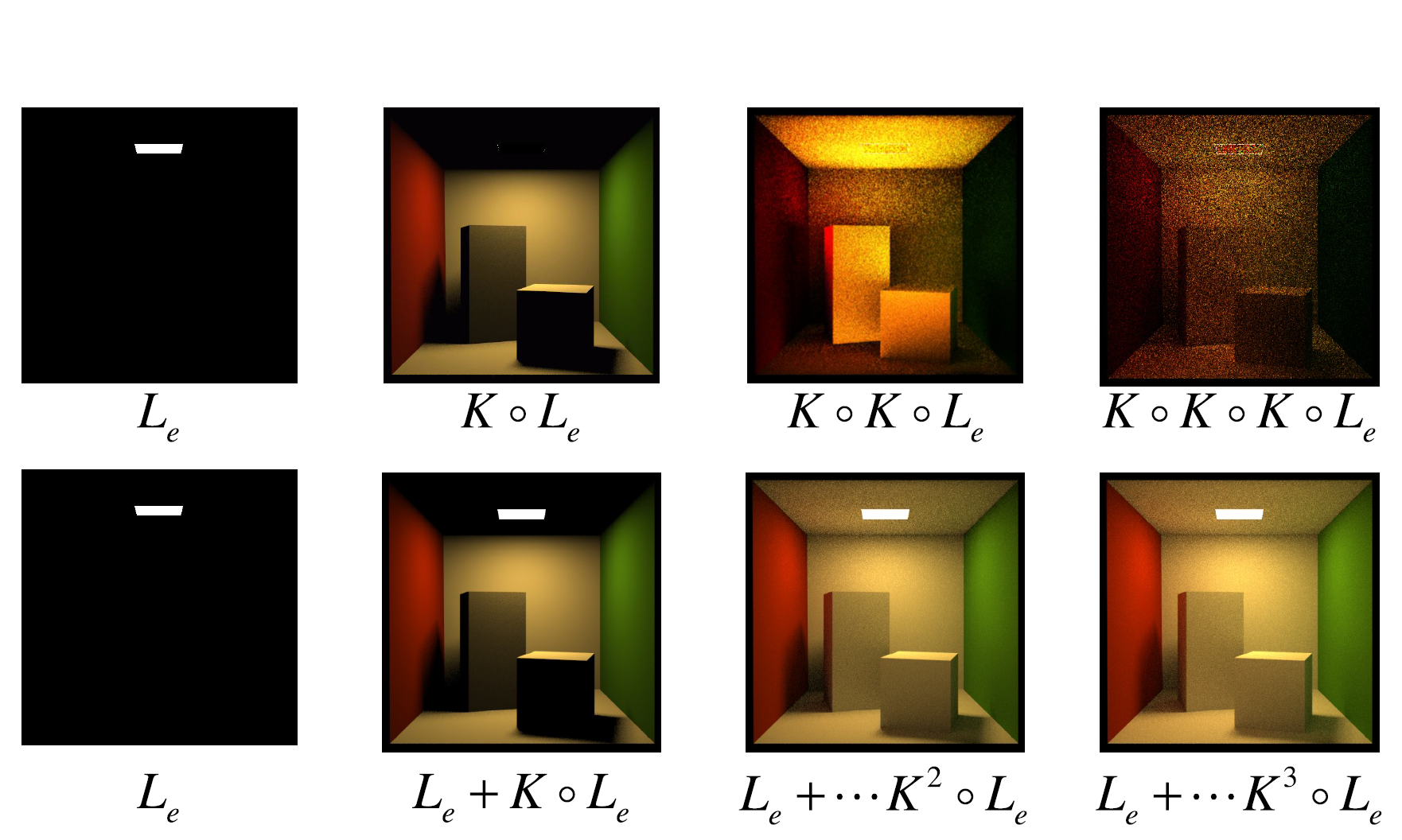
upload successful

这张图片可以用来形象地解释路径追踪的过程和渲染方程的递归思想。

  1. 光照传播的逐步过程（第一行） 从左到右展示了辐射亮度的逐步传播：

    • ( L_e )：直接显示光源自身的辐射亮度，没有经过任何反射（即场景中仅有光源可见）。
    • ( K \circ L_e )：光源辐射的光线被表面反射一次后产生的亮度分布。
    • ( K^2 \circ L_e )：光线经过两次反射后的亮度分布，逐步展现了间接光的贡献。
    • ( K^3 \circ L_e )：光线经过多次反射，渲染出更多的全局光照效果（如颜色溢出和柔和的阴影）。

    这清晰地展示了渲染方程的递归性质，即光的出射亮度由入射亮度决定，而入射亮度又是其他点的出射亮度。

  2. 累积全局光照（第二行） 从左到右展现了路径追踪中的逐步累积过程：

    • 左侧开始时，仍然仅有自发光亮度 ( L_e )。
    • 随着 ( K \circ L_e )、( K^2 \circ L_e ) 等逐步累积，全局光照效果逐渐完善。
    • 最右侧的最终图像 ( L_e + K \circ L_e + K^2 \circ L_e + K^3 \circ L_e ) 是对所有间接光和直接光的完整累积，逼真地表现了场景的光照效果。

  3. 每一列图片可以被视为路径追踪模拟的某种“深度”：

    • 第一列表示路径长度为 0，仅采样直接光源。
    • 第二列表示路径长度为 1，模拟光线反射一次。
    • 第三列和第四列逐步增加反射次数，从而更完整地捕捉场景的光照。

    图片中的噪点（特别是在高次反射部分）直观体现了蒙特卡洛方法的随机性和误差。噪点主要出现在高次反射（如 ( K^2 \circ L_e )、( K^3 \circ L_e )）部分，这是由于路径追踪在估算间接光照时，采样数量不足导致的。可以通过增加采样次数（路径追踪样本）来逐步去除噪点。

实时与高质量：渲染技术的两难抉择

交互式的实时渲染通常需要维持每秒 60 帧（FPS）或更高的帧率，这意味着每帧的渲染时间需要控制在 16 毫秒以内。而复杂场景高质量的路径追踪渲染往往需要几分钟甚至数小时才能完成一帧，因此实时渲染和高质量渲染在计算机图形学渲染技术中形成了难以调和的矛盾。

最新的研究热点：复用（Reusing）方法

最新的图形学研究热点之一是复用（Reusing）技术，它通过重复利用渲染过程中的中间数据或结果，减少计算需求以提升效率。典型方法包括：

  1. 光线路径复用：

    • 范围：在三维空间中进行复用。
    • 目标：在路径追踪过程中，重用已有的光线路径或与几何的交点数据，从而减少光线与场景求交的计算。
    • 应用：例如，在动态场景中重复使用静态场景中的路径数据，减少不必要的光线追踪。

  2. 样本复用：

    • 范围：在采样空间中进行复用。
    • 目标：优化蒙特卡洛采样，通过调整已有采样的权重或分布，避免浪费已有的样本数据。
    • 应用：例如，通过重采样技术降低噪声或在不同视角共享采样数据，减少全新的随机采样需求。

  3. 屏幕空间复用：

    • 范围：在屏幕空间（二维图像）中进行复用。
    • 目标：通过时间或空间上的数据共享，避免对屏幕像素的重复计算。
    • 应用：在实时渲染中，用前一帧的光照数据填补当前帧，或者通过相邻像素推导未采样像素的值。

总结与问答

计算机图形学渲染技术从简单的几何投影（如光栅化）发展到全面模拟光线传播（如路径追踪），实现了从快速的实时渲染到逼真的全局光照效果的跨越。以下是关键技术和特性的总结：

  1. 光栅化

    • 快速、硬件支持广泛，适合实时渲染。
    • 无法直接模拟反射、折射和间接光照，需手动实现。

  2. 光线投射

    • 简单实现直接光照，支持几何阴影的生成。
    • 不支持多次光线交互。

  3. 光线追踪

    • 支持反射和折射，部分实现真实光线传播。
    • 不足以模拟复杂间接光照。

  4. 路径追踪

    • 基于蒙特卡洛方法，完整解决渲染方程。
    • 高质量全局光照，计算成本极高。

  5. 最新研究热点

    • 复用技术：通过路径、样本和屏幕空间的复用，平衡实时性与高质量渲染。